|
Probability density function 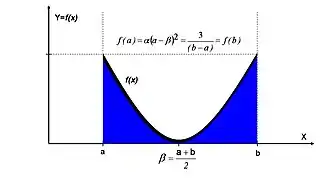 | |||
| Parameters |
or | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | TBD | ||
| MGF | See text | ||
| CF | See text | ||
In probability theory and statistics, the U-quadratic distribution is a continuous probability distribution defined by a unique convex quadratic function with lower limit a and upper limit b.
Parameter relations
This distribution has effectively only two parameters a, b, as the other two are explicit functions of the support defined by the former two parameters:
(gravitational balance center, offset), and
(vertical scale).
Related distributions
One can introduce a vertically inverted ()-quadratic distribution in analogous fashion.
Applications
This distribution is a useful model for symmetric bimodal processes. Other continuous distributions allow more flexibility, in terms of relaxing the symmetry and the quadratic shape of the density function, which are enforced in the U-quadratic distribution – e.g., beta distribution and gamma distribution.
Moment generating function
Characteristic function
Beamforming
The quadratic U and inverted quadratic U distribution has an application to beamforming and pattern synthesis.[1][2]
References
- ↑ Buchanan, Kristopher; Wheeland, Sara (July 2022). "Comparison of the Quadratic U and Inverse Quadratic U Sum-Difference Beampatterns". 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI). pp. 1828–1829. doi:10.1109/AP-S/USNC-URSI47032.2022.9887273. ISBN 978-1-6654-9658-2. S2CID 252411058.
- ↑ Buchanan, Kristopher; Wheeland, Sara (July 2022). "Investigation of the Sum-Difference Beampatterns Using the Quadratic U Distribution". 2022 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (AP-S/URSI). pp. 135–136. doi:10.1109/AP-S/USNC-URSI47032.2022.9886771. ISBN 978-1-6654-9658-2. S2CID 252410725.