Kaniadakis Gamma distribution

κ-Gamma distribution
	Probability density function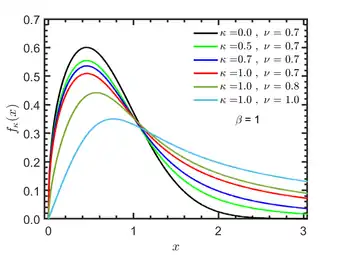
Parameters	; shape (real) ; rate (real) ;
Support
PDF
CDF
Mode
Method of Moments

The Kaniadakis Generalized Gamma distribution (or κ-Generalized Gamma distribution) is a four-parameter family of continuous statistical distributions, supported on a semi-infinite interval [0,∞), which arising from the Kaniadakis statistics. It is one example of a Kaniadakis distribution. The κ-Gamma is a deformation of the Generalized Gamma distribution.

Definitions

Probability density function

The Kaniadakis κ-Gamma distribution has the following probability density function:^[1]

f_{_{\kappa }}(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1}\exp _{\kappa }(-\beta x^{\alpha })

valid for $x\geq 0$ , where $0\leq |\kappa |<1$ is the entropic index associated with the Kaniadakis entropy, $0<\nu <1/\kappa$ , $\beta >0$ is the scale parameter, and $\alpha >0$ is the shape parameter.

The ordinary generalized Gamma distribution is recovered as $\kappa \rightarrow 0$ : $f_{_{0}}(x)={\frac {|\alpha |\beta ^{\nu }}{\Gamma \left(\nu \right)}}x^{\alpha \nu -1}\exp _{\kappa }(-\beta x^{\alpha })$ .

Cumulative distribution function

The cumulative distribution function of κ-Gamma distribution assumes the form:

F_{\kappa }(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}\int _{0}^{x}z^{\alpha \nu -1}\exp _{\kappa }(-\beta z^{\alpha })dz

valid for $x\geq 0$ , where $0\leq |\kappa |<1$ . The cumulative Generalized Gamma distribution is recovered in the classical limit $\kappa \rightarrow 0$ .

Properties

Moments and mode

The κ-Gamma distribution has moment of order $m$ given by^[1]

\operatorname {E} [X^{m}]=\beta ^{-m/\alpha }{\frac {(1+\kappa \nu )(2\kappa )^{-m/\alpha }}{1+\kappa {\big (}\nu +{\frac {m}{\alpha }}{\big )}}}{\frac {\Gamma {\big (}\nu +{\frac {m}{\alpha }}{\big )}}{\Gamma (\nu )}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\Big )}}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}-{\frac {m}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}+{\frac {m}{2\alpha }}{\Big )}}}

The moment of order $m$ of the κ-Gamma distribution is finite for $0<\nu +m/\alpha <1/\kappa$ .

The mode is given by:

x_{\textrm {mode}}=\beta ^{-1/\alpha }{\Bigg (}\nu -{\frac {1}{\alpha }}{\Bigg )}^{\frac {1}{\alpha }}{\Bigg [}1-\kappa ^{2}{\bigg (}\nu -{\frac {1}{\alpha }}{\bigg )}^{2}{\Bigg ]}^{-{\frac {1}{2\alpha }}}

Asymptotic behavior

The κ-Gamma distribution behaves asymptotically as follows:^[1]

\lim _{x\to +\infty }f_{\kappa }(x)\sim (2\kappa \beta )^{-1/\kappa }(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1-\alpha /\kappa }

\lim _{x\to 0^{+}}f_{\kappa }(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1}

Related distributions

The κ-Gamma distributions is a generalization of:
- κ-Exponential distribution of type I, when $\alpha =\nu =1$ ;
- Kaniadakis κ-Erlang distribution, when $\alpha =1$ and $\nu =n=$ positive integer.
- κ-Half-Normal distribution, when $\alpha =2$ and $\nu =1/2$ ;
A κ-Gamma distribution corresponds to several probability distributions when $\kappa =0$ $\kappa = 0$ , such as:
- Gamma distribution, when $\alpha =1$ ;
- Exponential distribution, when $\alpha =\nu =1$ ;
- Erlang distribution, when $\alpha =1$ and $\nu =n=$ positive integer;
- Chi-Squared distribution, when $\alpha =1$ and $\nu =$ half integer;
- Nakagami distribution, when $\alpha =2$ and $\nu >0$ ;
- Rayleigh distribution, when $\alpha =2$ and $\nu =1$ ;
- Chi distribution, when $\alpha =2$ and $\nu =$ half integer;
- Maxwell distribution, when $\alpha =2$ and $\nu =3/2$ ;
- Half-Normal distribution, when $\alpha =2$ and $\nu =1/2$ ;
- Weibull distribution, when $\alpha >0$ and $\nu =1$ ;
- Stretched Exponential distribution, when $\alpha >0$ and $\nu =1/\alpha$ ;

References

1 2 3 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.

External links

Kaniadakis Statistics on arXiv.org

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] 1 2 3 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.

[1]