The Kaniadakis exponential distribution (or κ-exponential distribution) is a probability distribution arising from the maximization of the Kaniadakis entropy under appropriate constraints. It is one example of a Kaniadakis distribution. The κ-exponential is a generalization of the exponential distribution in the same way that Kaniadakis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy.[1] The κ-exponential distribution of Type I is a particular case of the κ-Gamma distribution, whilst the κ-exponential distribution of Type II is a particular case of the κ-Weibull distribution.
Type I
Probability density function
|
Probability density function  | |||
|
Cumulative distribution function 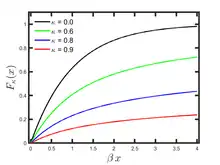 | |||
| Parameters |
shape (real) rate (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Method of Moments | |||
The Kaniadakis κ-exponential distribution of Type I is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics which exhibit power-law tails. This distribution has the following probability density function:[2]
valid for , where is the entropic index associated with the Kaniadakis entropy and is known as rate parameter. The exponential distribution is recovered as
Cumulative distribution function
The cumulative distribution function of κ-exponential distribution of Type I is given by
for . The cumulative exponential distribution is recovered in the classical limit .
Properties
Moments, expectation value and variance
The κ-exponential distribution of type I has moment of order given by[2]
where is finite if .
The expectation is defined as:
and the variance is:
Kurtosis
The kurtosis of the κ-exponential distribution of type I may be computed thought:
Thus, the kurtosis of the κ-exponential distribution of type I distribution is given by:
or
The kurtosis of the ordinary exponential distribution is recovered in the limit .
Skewness
The skewness of the κ-exponential distribution of type I may be computed thought:
Thus, the skewness of the κ-exponential distribution of type I distribution is given by:
The kurtosis of the ordinary exponential distribution is recovered in the limit .
Type II
Probability density function
|
Probability density function  | |||
|
Cumulative distribution function 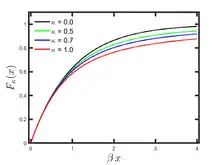 | |||
| Parameters |
shape (real) rate (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Method of Moments | |||
The Kaniadakis κ-exponential distribution of Type II also is part of a class of statistical distributions emerging from the Kaniadakis κ-statistics which exhibit power-law tails, but with different constraints. This distribution is a particular case of the Kaniadakis κ-Weibull distribution with is:[2]
valid for , where is the entropic index associated with the Kaniadakis entropy and is known as rate parameter.
The exponential distribution is recovered as
Cumulative distribution function
The cumulative distribution function of κ-exponential distribution of Type II is given by
for . The cumulative exponential distribution is recovered in the classical limit .
Properties
Moments, expectation value and variance
The κ-exponential distribution of type II has moment of order given by[2]
The expectation value and the variance are:
The mode is given by:
Kurtosis
The kurtosis of the κ-exponential distribution of type II may be computed thought:
Thus, the kurtosis of the κ-exponential distribution of type II distribution is given by:
or
Skewness
The skewness of the κ-exponential distribution of type II may be computed thought:
Thus, the skewness of the κ-exponential distribution of type II distribution is given by:
or
The skewness of the ordinary exponential distribution is recovered in the limit .
Quantiles
The quantiles are given by the following expression
with , in which the median is the case :
Lorenz curve
The Lorenz curve associated with the κ-exponential distribution of type II is given by:[2]
The Gini coefficient is
Asymptotic behavior
The κ-exponential distribution of type II behaves asymptotically as follows:[2]
Applications
The κ-exponential distribution has been applied in several areas, such as:
- In geomechanics, for analyzing the properties of rock masses;[3]
- In quantum theory, in physical analysis using Planck's radiation law;[4]
- In inverse problems, the κ-exponential distribution has been used to formulate a robust approach;[5]
- In Network theory.[6]
See also
References
- ↑ Kaniadakis, G. (2001). "Non-linear kinetics underlying generalized statistics". Physica A: Statistical Mechanics and Its Applications. 296 (3–4): 405–425. arXiv:cond-mat/0103467. Bibcode:2001PhyA..296..405K. doi:10.1016/S0378-4371(01)00184-4. S2CID 44275064.
- 1 2 3 4 5 6 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.
- ↑ Oreste, Pierpaolo; Spagnoli, Giovanni (2018-04-03). "Statistical analysis of some main geomechanical formulations evaluated with the Kaniadakis exponential law". Geomechanics and Geoengineering. 13 (2): 139–145. doi:10.1080/17486025.2017.1373201. ISSN 1748-6025. S2CID 133860553.
- ↑ Ourabah, Kamel; Tribeche, Mouloud (2014). "Planck radiation law and Einstein coefficients reexamined in Kaniadakis κ statistics". Physical Review E. 89 (6): 062130. Bibcode:2014PhRvE..89f2130O. doi:10.1103/PhysRevE.89.062130. ISSN 1539-3755. PMID 25019747.
- ↑ da Silva, Sérgio Luiz E. F.; dos Santos Lima, Gustavo Z.; Volpe, Ernani V.; de Araújo, João M.; Corso, Gilberto (2021). "Robust approaches for inverse problems based on Tsallis and Kaniadakis generalised statistics". The European Physical Journal Plus. 136 (5): 518. Bibcode:2021EPJP..136..518D. doi:10.1140/epjp/s13360-021-01521-w. ISSN 2190-5444. S2CID 236575441.
- ↑ Macedo-Filho, A.; Moreira, D.A.; Silva, R.; da Silva, Luciano R. (2013). "Maximum entropy principle for Kaniadakis statistics and networks". Physics Letters A. 377 (12): 842–846. Bibcode:2013PhLA..377..842M. doi:10.1016/j.physleta.2013.01.032.