|
Probability density function 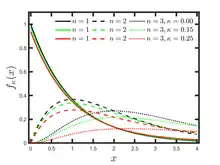 Plot of the κ-Erlang distribution for typical κ-values and n=1, 2,3. The case κ=0 corresponds to the ordinary Erlang distribution. | |||
| Parameters |
| ||
|---|---|---|---|
| Support | |||
| CDF | |||
The Kaniadakis Erlang distribution (or κ-Erlang Gamma distribution) is a family of continuous statistical distributions, which is a particular case of the κ-Gamma distribution, when and positive integer.[1] The first member of this family is the κ-exponential distribution of Type I. The κ-Erlang is a κ-deformed version of the Erlang distribution. It is one example of a Kaniadakis distribution.
Characterization
Probability density function
The Kaniadakis κ-Erlang distribution has the following probability density function:[1]
valid for and , where is the entropic index associated with the Kaniadakis entropy.
The ordinary Erlang Distribution is recovered as .
Cumulative distribution function
The cumulative distribution function of κ-Erlang distribution assumes the form:[1]
valid for , where . The cumulative Erlang distribution is recovered in the classical limit .
Survival distribution and hazard functions
The survival function of the κ-Erlang distribution is given by:
The survival function of the κ-Erlang distribution enables the determination of hazard functions in closed form through the solution of the κ-rate equation:
where is the hazard function.
Family distribution
A family of κ-distributions arises from the κ-Erlang distribution, each associated with a specific value of , valid for and . Such members are determined from the κ-Erlang cumulative distribution, which can be rewritten as:
where
with
First member
The first member () of the κ-Erlang family is the κ-Exponential distribution of type I, in which the probability density function and the cumulative distribution function are defined as:
Second member
The second member () of the κ-Erlang family has the probability density function and the cumulative distribution function defined as:
Third member
The second member () has the probability density function and the cumulative distribution function defined as:
Related distributions
- The κ-Exponential distribution of type I is a particular case of the κ-Erlang distribution when ;
- A κ-Erlang distribution corresponds to am ordinary exponential distribution when and ;
See also
References
- 1 2 3 Kaniadakis, G. (2021-01-01). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.