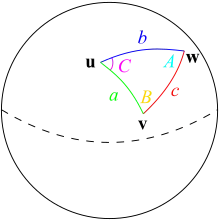
In spherical trigonometry, the half side formula relates the angles and lengths of the sides of spherical triangles, which are triangles drawn on the surface of a sphere and so have curved sides and do not obey the formulas for plane triangles.[1]
For a triangle on a sphere, the half-side formula is[2]
where a, b, c are the angular lengths (measure of central angle, arc lengths normalized to a sphere of unit radius) of the sides opposite angles A, B, C respectively, and is half the sum of the angles. Two more formulas can be obtained for and by permuting the labels
The polar dual relationship for a spherical triangle is the half-angle formula,
where semiperimeter is half the sum of the sides. Again, two more formulas can be obtained by permuting the labels
Half-tangent variant
The same relationships can be written as rational equations of half-tangents (tangents of half-angles). If and then the half-side formula is equivalent to:
and the half-angle formula is equivalent to:
See also
References
- ↑ Bronshtein, I. N.; Semendyayev, K. A.; Musiol, Gerhard; Mühlig, Heiner (2007), Handbook of Mathematics, Springer, p. 165, ISBN 9783540721222
- ↑ Nelson, David (2008), The Penguin Dictionary of Mathematics (4th ed.), Penguin UK, p. 529, ISBN 9780141920870.