In mathematics, a dendrite is a certain type of topological space that may be characterized either as a locally connected dendroid or equivalently as a locally connected continuum that contains no simple closed curves.[1]
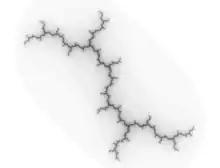
Dendrite Julia set
Importance
Dendrites may be used to model certain types of Julia set.[2] For example, if 0 is pre-periodic, but not periodic, under the function , then the Julia set of is a dendrite: connected, without interior.[3]
References
- ↑ Whyburn, Gordon Thomas (1942), Analytic Topology, American Mathematical Society Colloquium Publications, vol. 28, New York: American Mathematical Society, p. 88, MR 0007095.
- ↑ Carleson, Lennart; Gamelin, Theodore W. (1993), Complex Dynamics, Universitext, vol. 69, Springer, p. 94, ISBN 9780387979427.
- ↑ Devaney, Robert L. (1989), An Introduction to Chaotic Dynamical Systems, Studies in Nonlinearity, Addison-Wesley Publishing Company, p. 294, MR 1046376.
See also
Wikimedia Commons has media related to Dendrite Julia sets.
- Misiurewicz point
- Real tree, a related concept defined using metric spaces instead of topological spaces
- Dendroid (topology) and unicoherent space, two more general types of tree-like topological space
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.