| ||||
|---|---|---|---|---|
| Cardinal | seventy-three | |||
| Ordinal | 73rd (seventy-third) | |||
| Factorization | prime | |||
| Prime | 21st | |||
| Divisors | 1, 73 | |||
| Greek numeral | ΟΓ´ | |||
| Roman numeral | LXXIII | |||
| Binary | 10010012 | |||
| Ternary | 22013 | |||
| Senary | 2016 | |||
| Octal | 1118 | |||
| Duodecimal | 6112 | |||
| Hexadecimal | 4916 | |||
73 (seventy-three) is the natural number following 72 and preceding 74. In English, it is the smallest natural number with twelve letters in its spelled out name.
In mathematics
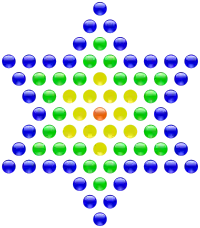
73 is the 21st prime number, and emirp with 37, the 12th prime number.[1] It is also the eighth twin prime, with 71. It is the largest minimal primitive root in the first 100,000 primes; in other words, if p is one of the first one hundred thousand primes, then at least one of the numbers 2, 3, 4, 5, 6, ..., 73 is a primitive root modulo p. 73 is also the smallest factor of the first composite generalized Fermat number in decimal: , and the smallest prime congruent to 1 modulo 24, as well as the only prime repunit in octal (1118). It is the fourth star number.[2]
Sheldon prime
Notably, 73 is the only Sheldon prime to contain both "mirror" and "product" properties:[3]
- 73, as an emirp, has 37 as its dual permutable prime, a mirroring of its base ten digits, 7 and 3. 73 is the 21st prime number, while 37 is the 12th, which is a second mirroring; and
- 73 has a prime index of 21 = 7 × 3; a product property where the product of its base-10 digits is precisely its index in the sequence of prime numbers.
Arithmetically, from sums of 73 and 37 with their prime indexes, one obtains:
Meanwhile,
- 73 and 37 are lucky primes and sexy primes, both twice over.[4][5][6] They are also successive Pierpont primes, respectively the 9th and 8th.[7]
- 73 and 37 are consecutive star numbers and equivalently consecutive centered dodecagonal (12-gonal) numbers, respectively the 4th and the 3rd.[2]
- 73 and 37 are successive values of such that every positive integer can be written as the sum of 73 or fewer sixth powers, or 37 or fewer fifth powers (see Waring's problem).[8]
- 73 and 37 are consecutive primes in the 7-integer covering set of the first known Sierpinski number 78,557, of the form composite for all natural numbers , with 73 as its largest group member: {3, 5, 7, 13, 19, 37, 73}.
Consider the following sequence :[9]- Let be a Sierpiński number or Riesel number divisible by , and let be the largest number in a set of primes which cover every number of the form or of the form , with ;
- equals if and only if there exists no number that has a covering set with largest prime greater than .
Known such index values where is equal to 73 as the largest member of such covering sets are: {1, 6, 9, 12, 15, 16, 21, 22, 24, and 27}, with 37 present alongside 73. In particular, ≥ 73 for any .
- 73 and 37 have a range of 37 numbers, inclusive of both 37 and 73; their difference, on the other hand, is 36, or thrice 12. Also,
777 = 3 × 37 × 7 = 21 × 37, where 37 is a concatenation of 3 and 7.
703 equals the sum of the first 37 non-zero positive integers, equivalently the 37th triangular number.[10] The harmonic mean of its divisors is 3.7.
373 has a prime index of 74, or twice 37.[11] Like 73 and 37, 373 is a permutable prime alongside 337 and 733, the second of three trios of three-digit permutable primes in decimal.[12] 337 is also the eighth star number.[2]
- 337 + 373 + 733 = 1443, the number of edges in the join of two cycle graphs of order 37.[13]
343 = 7 × 7 × 7 = 73: the cube of 7, or 7 cubed, wherein replacing two neighboring digits with their digit sums 3 + 4 and 4 + 3 yields 37 : 73.
- Also, the product of neighboring digits 3 × 4 is 12, like 4 × 3, while the sum of its prime factors 7 + 7 + 7 is 21.
In binary 73 is represented as 1001001, while 21 in binary is 10101, with 7 and 3 represented as 111 and 11 respectively; all which are palindromic. Of the seven binary digits representing 73, there are three 1s. In addition to having prime factors 7 and 3, the number 21 represents the ternary (base-3) equivalent of the decimal numeral 7, that is to say: 213 = 710.
Other properties
73 is one of the fifteen left-truncatable and right-truncatable primes in decimal, meaning it remains prime when the last "right" digit is successively removed and it remains prime when the last "left" digit is successively removed; and because it is a twin prime (with 71), it is the only two-digit twin prime that is both a left-truncatable and right-truncatable prime.
The row sum of Lah numbers of the form with and is equal to .[14] These numbers represent coefficients expressing rising factorials in terms of falling factorials, and vice-versa; equivalently in this case to the number of partitions of into any number of lists, where a list means an ordered subset.[15]
73 requires 115 steps to return to 1 in the Collatz problem, and 37 requires 21: {37, 112, 56, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1}.[16] Collectively, the sum between these steps is 136, the 16th triangular number, where {16, 8, 4, 2, 1} is the only possible step root pathway.[17]
There are 73 three-dimensional arithmetic crystal classes that are part of 230 crystallographic space group types.[18] These 73 groups are specifically symmorphic groups such that all operating lattice symmetries have one common fixed isomorphic point, with the remaining 157 groups nonsymmorphic (the 37th prime is 157).
In five-dimensional space, there are 73 Euclidean solutions of 5-polytopes with uniform symmetry, excluding prismatic forms: 19 from the simplex group, 23 from the demihypercube group, and 31 from the hypercubic group, of which 15 equivalent solutions are shared between and from distinct polytope operations.
In moonshine theory of sporadic groups, 73 is the first non-supersingular prime greater than 71 that does not divide the order of the largest sporadic group . All primes greater than or equal to 73 are non-supersingular, while 37, on the other hand, is the smallest prime number that is not supersingular.[19] contains a total of 194 conjugacy classes that involve 73 distinct orders (without including multiplicities over which letters run).[20]
73 is the largest member of a 17-integer matrix definite quadratic that represents all prime numbers: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 67, 73}.[21]
In science
- The atomic number of tantalum
In astronomy
- Messier object M73, a magnitude 9.0 apparent open cluster in the constellation Aquarius.
- The New General Catalogue object NGC 73, a barred spiral galaxy in the constellation Cetus.
- The number of seconds it took for the Space Shuttle Challenger OV-099 shuttle to explode after launch.
- 73 is the number of rows in the 1,679-bit Arecibo message, sent to space in search for extraterrestrial intelligence.
In chronology
In other fields
73 is also:
- The number of books in the Catholic Bible.[22]
- Amateur radio operators and other morse code users commonly use the number 73 as a "92 Code" abbreviation for "best regards", typically when ending a QSO (a conversation with another operator). These codes also facilitate communication between operators who may not be native English speakers.[23] In Morse code, 73 is an easily recognized palindrome: ( - - · · · · · · - - ).
- 73 (also known as 73 Amateur Radio Today) was an amateur radio magazine published from 1960 to 2003.
- 73 was the number on the Torpedo Patrol (PT) boat in the TV show McHale's Navy.
- The registry of the U.S. Navy's nuclear aircraft carrier USS George Washington (CVN-73), named after U.S. President George Washington.
- No. 73 was the name of a 1980s children's television programme in the United Kingdom. It ran from 1982 to 1988 and starred Sandi Toksvig.
- Pizza 73 is a Canadian pizza chain.
- Game show Match Game '73 in 1973.
- Fender Rhodes Stage 73 Piano.
- Sonnet 73 by William Shakespeare.
- The number of the French department Savoie.
- On a CB radio, 10-73 means "speed trap at..."
In sports
- In international curling competitions, each side is given 73 minutes to complete all of its throws.
- In baseball, the single-season home run record set by Barry Bonds in 2001.
- In basketball, the number of games the Golden State Warriors won in the 2015–16 season (73–9), the most wins in NBA history.
- NFL: In the 1940 NFL championship game, the Bears beat the Redskins 73–0, the largest score ever in an NFL game. (The Redskins won their previous regular season game, 7–3.)
Popular culture
The Big Bang Theory
73 is Sheldon Cooper's favorite number in The Big Bang Theory. He first expresses his love for it in "The Alien Parasite Hypothesis, the 73rd episode of The Big Bang Theory.".[24] Jim Parsons was born in the year 1973.[25] He often wears a t-shirt with the number 73 on it.[26]
See also
References
- ↑ "Sloane's A006567 : Emirps". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-29.
- 1 2 3 "Sloane's A003154 : Centered 12-gonal numbers. Also star numbers: 6*n*(n-1) + 1". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-05-29.
- ↑ Pomerance, Carl; Spicer, Chris (February 2019). "Proof of the Sheldon conjecture" (PDF). American Mathematical Monthly. 126 (8): 688–698. doi:10.1080/00029890.2019.1626672. S2CID 204199415.
- ↑ Sloane, N. J. A. (ed.). "Sequence A031157 (Numbers that are both lucky and prime.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-14.
- ↑ Sloane, N. J. A. (ed.). "Sequence A023201 (Primes p such that p + 6 is also prime. (Lesser of a pair of sexy primes.))". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-14.
- ↑ Sloane, N. J. A. (ed.). "Sequence A046117 (Primes p such that p-6 is also prime. (Upper of a pair of sexy primes.))". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-14.
- ↑ Sloane, N. J. A. (ed.). "Sequence A005109 (Class 1- (or Pierpont) primes)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-12-19.
- ↑ Sloane, N. J. A. (ed.). "Sequence A002804 ((Presumed) solution to Waring's problem)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ Sloane, N. J. A. (ed.). "Sequence A305473 (Let k be a Sierpiński or Riesel number divisible by 2*n – 1...)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-13.
- ↑ Sloane, N. J. A. (ed.). "Sequence A000217 (Triangular numbers.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-13.
- ↑ Sloane, N. J. A. (ed.). "Sequence A000040 (The prime numbers.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-13.
- ↑ Sloane, N. J. A. (ed.). "Sequence A003459 (Absolute primes (or permutable primes): every permutation of the digits is a prime.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-13.
- ↑ "Sloane's A005563 : a(n) = n*(n+2) = (n+1)^2 – 1". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-15.
Number of edges in the join of two cycle graphs, both of order n, C_n * C_n.
- ↑ Riordan, John (1968). Combinatorial Identities. John Wiley & Sons. p. 194. LCCN 67031375. MR 0231725. OCLC 681863847.
- ↑ Sloane, N. J. A. (ed.). "Sequence A000262 (Number of "sets of lists": number of partitions of {1,...,n} into any number of lists, where a list means an ordered subset.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-09-02.
- ↑ Sloane, N. J. A. (ed.). "Sequence A006577 (Number of halving and tripling steps to reach 1 in '3x+1' problem, or -1 if 1 is never reached.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-09-18.
- ↑ Sloane, N. J. A. "3x+1 problem". The On-Line Encyclopedia of Integer Sequences. The OEIS Foundation. Retrieved 2023-09-18.
- ↑ Sloane, N. J. A. (ed.). "Sequence A004027 (Number of arithmetic n-dimensional crystal classes.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-11-29.
- ↑ Sloane, N. J. A. (ed.). "Sequence A002267 (The 15 supersingular primes)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-10-13.
- ↑ He, Yang-Hui; McKay, John (2015). "Sporadic and Exceptional". p. 20. arXiv:1505.06742 [math.AG].
- ↑ Sloane, N. J. A. (ed.). "Sequence A154363 (Numbers from Bhargava's prime-universality criterion theorem)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ↑ "Catholic Bible 101". Catholic Bible 101. Retrieved 16 September 2018.
- ↑ "Ham Radio History".
- ↑ "The Big Bang Theory (TV Series) - The Alien Parasite Hypothesis (2010) - Jim Parsons: Sheldon Cooper". IMDb. Retrieved 13 March 2023.
- ↑ "Jim Parsons". IMDb.
- ↑ "The Alien Parasite Hypothesis". The Big Bang Theory. Season 4. Episode 10.