A quasi-triangulation is a subdivision of a geometric object into simplices, where vertices are not points but arbitrary sloped line segments.[1] This division is not a triangulation in the geometric sense. It is a topological triangulation, however. A quasi-triangulation may have some of the characteristics of a Delaunay triangulation.
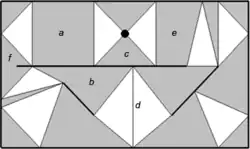
Quasi-triangulation. Line segments of the topology (quasi-vertices) are shown in black, gray — quasi-edges, white — faces. a — a convex quadrangular edge,
b — a nonconvex quadrangular edge, c — a triangular edge, d — a degenerate edge, a and e — parallel edges,
f — a quasi-edge contains a part of the line segment.
References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.